Notice on the Formula of Speed (velocity)
(On from Mad Maths)
I ask a mathematician
v(i)=t/d vs. v=d/t
or
"a minute for a mile"
vs.
"a mile in a minute"
Which is better? Which is right?
Speed has been measured throughout the ages.
And although the first formula above:
v(i)=t/d or "time per distance"
is instinctively used in human context to this day, and so most probably has been for thousands of years (how long did you take? how fast will they be here?),
as it is easy to add a sum of relative times t (moving, pausing, moving slower...) in relation to a set (or invariable) and known distance d,
the inverted formula:
v=d/t or "distance per time"
which is said to have been found by Galileo or his surroundings no longer than half a millennium ago, although counter- intuitive, is much more useful to describe a mechanical, physical, engineered movement, where time t is absolute (or invariable) and distance d is relative.
Whereas before there was a “negative” correlation between the propelling force or action, like the pull of a bow, and the reaction to it - the stronger the force, the shorter the time for the arrow to reach its destiny - there is now a “positive” correlation between the propelling force, the speed of the arrow, and the distance it will fly.
Beyond that, the new formula also elegantly bypasses the issue of a possible zero denominator, as the distance d can be zero, as during immobility, but time t goes on relentless.
Now here’s the Question:
Could you, mathematically and physically, still use the former?
And could you, in consequence, turn any physical formula on its head, and still be able to use it?
Like, perhaps, the ancient basic formula for entropy?
I was able to forward my question about this problem to a professor of mathematics, and his answer was, as to be expected, professional.
POSING THE PROBLEM:
If two quantities (A and B) are related by a factor (x,y,z...), this can be expressed as
A=xB or B=yA,
or transformed as
x=A/B or y=B /A [here with y=1/x]
Up to here, everyone is free to choose either A/B or B/A to express the ratio of these quantities.
Is that correct up to here?
[No Answer; possibly too trivial]
If correct so far:
If, for example, A (independent of B) as a physical quantity (distance, time...) can theoretically assume the value 0, then the expression y=B/A is not defined at this point, and is therefore ruled out as a possibility
In this case, however, the expression x=A/B can and may be used without further ado, since one is free to choose the ratio; the entire expression then has the value 0.
In the case of the theoretical possibility of B=0, the reverse is the case.
- - - -Is there a mistake in reasoning up to this point?
Or is that, so far, a general statement?
As a concrete example:
The speed of a moving object, as the ratio of the distance d covered to the time t required, can either be expressed
as v(x)=t/s (x hours per kilometer)
or v(y)=s/t (y kilometers per hour)
In the case of v(x)=t/s, v is not defined at the point s=0 (standstill), and is therefore generally excluded as an applicable formula.
In contrast, the freely selectable, equally valid alternative v(y)=s/t would not be defined at the point t=0 (simultaneity).
However, this possibility is theoretically ruled out (the time taken for an object to move can never be zero).
Physics and mathematics confirm each other in this case.
So, the formula v=s/t, or kilometers per hour, is applicable.
[One could even require that a 0 in the numerator must in principle be physically possible; this would also be given in v=s/t, but not given in v=t/s]Generally speaking, this approach would apply to any such relationship.
------
His answer to this was, in general, that:
The quotient A/B is indeed defined for all numbers A and all numbers B =/= 0
For A =/= 0, A/0 is occasionally defined as infinite, while the quotient 0/0 is undetermined, although a value is sometimes (arbitrarily) assumed to it as well.
If A and B are physical quantities, the same applies, e. g. for velocity v=distance/time or acceleration a=distance/time²; and of course,
these values only make sense if the denominator is different from 0.However, a formula (e.g. with a quotient) does not have to be wrong or pointless, just because it is not defined for all values of a possible domain (e.g. for the value 0 in the denominator).
In that case, what sometimes helps is a limit value consideration, e.g. for the speed:
v(t) = s(t) /t (to be correct, the first derivative should actually be here),
and
v(0) = lim s(t)/t.
t -> 0
He did not touch upon the subject of my first assertion, that (at the beginning) you can freely choose the description of a ratio of A to B with x=A/B or y=B/A, so long as you don't know anything about any possible points of zero - but no longer after that.
Perhaps that part was just too trivial.
But the second part is exactly the point.
If its value can actually assume 0, as it happens in nature and physics, for example with a length of 0, then this quantity must not appear in the denominator of a formula; otherwise the result at that point (and thus also in the immediate vicinity) is not meaningful or usable.
In this case, however, one could possibly work with the reciprocal value, i.e. turn the fraction upside down; this means that this critical quantity is now in the numerator, while the numerical ratio itself has not changed.
Or to put it another way:
The distinction as to whether a (single) zero value could turn up either in the numerator, or in the denominator, could be used as a litmus test to determine whether one is using the right or the wrong (rather: the less favorable) one of two equally possible, but to each other reciprocal formulas.
The formulas for speed v=distance/time or acceleration a=distance/time² are correct in this sense, because, in reality, the time of a movement can never be 0; the denominator can therefore not, not even theoretically, physically ever assume zero.
Which then conforms to the rules of mathematics: no zero in the denominator. Ever.
The alternative, reciprocal formula for velocity, v(i) = time/distance, which would also be theoretically possible, would be wrongly chosen, because the distance of a movement (here in the denominator!) can physically indeed assume 0: namely in the case of immobility. And that, again, is mathematically not allowed.
And so, immobility would be mathematically not allowed, while it exists physically.
Consequences
The question, now, is whether you can turn the tables and say:
"If any physical formula could even POSSIBLY have a zero in the denominator, if only even theoretically, then that formula is wrong (or rather, the wrong choice); and one should try their inversion."
And, as already mentioned, in my opinion there is (at least) one candidate for this, namely the formula for entropy.
Physics has built a huge, impenetrable barrier around it for the last 150 years, in order to be able to calculate with it, because with S=Q/T entropy would be very high in large areas of the universe, where the temperature T, positioned in the denominator, is close to 0.
However, if you turn the formula on its head, with S(i)=T/Q, entropy not only makes semantic sense, namely the temperature as an indicator of the energy already converted in relation to the energy potential still available,* it also increases steadily with further energy conversion, and the description of the universe, from its beginnings to a contemporary burning candle, becomes downright simple (and one no longer has to fabulate about 'heat supply' or such instead of 'heat generation').
Entropy at T=0 is then simply 0 itself - and Q=0 in the denominator could physically only exists with T=0 in the numerator simultaneously, and thus 0/0, which is mathematically undetermined, as declared above; as well as physically. Nothing by nothing is - nothing.
* [To which there may be to add: There is also the circumstance that in thermodynamics, Q, or the amount of energy, is unchangeable, as mass and energy will be conserved; heat, too, is a form of energy. The amount of energy, therefore, and not the temperature, is the absolute quantity and is probably (for that alone!) best placed in the denominator, as time is in the formula for velocity or speed.]
Not only does calculating the universe then become easier; the emergence of life also follows, with a little extra, almost by itself; far from being a theoretical improbability, it turns into an unavoidable necessity - and that the original, possibly incorrectly chosen description of entropy falls into the life and creative period of Darwin and Marx is probably more important than one is inclined to believe: Life is work, every heartbeat, and thus falls under the laws of thermodynamics, whether one likes it or not; while evolution (even the pre-biological one!), on balance, increases and accumulates information, and does not reduce or distribute it.
We are indeed poking around inside the headquarters here; but that is part of the fun.
So, all in all, my assertions, above, were not refuted; instead, they were deemed unnecessary, as mathematics, the queen of science, can handle the problem of using a formula that may not be defined for all possible values.
[Which lies within the realm of "any problem" :-)]
However, in reality or physics, “these values only make sense if the denominator is different from 0”.
Natura non facit salta; material nature abhors a vacuum (i. e. an undefined area) and does not jump around it.
Any which way, I came to this junction of physics and math from quite the other direction:
It was after I had become aware of the presence of the second component, namely gravity, as prerequisite of the dual complementary system of gravity and thermodynamics, the problem of zero entropy popped up as a stumbling block; and so the solution, to turn the formula on its head, was a possible result of that model, and not a prerequisition for it.
It's an "Indiana Jones" setting.
The problem has two components, one mathematical (am I allowed to do this?) and one physical (what would that change?)
The math part is a small stone idol; the physics part is the huge stone cave temple door. I think it will open that door, if I am allowed to turn the idol (the formula) on its head, and use that as a key to unlock the door to the temple holding untold riches (this has been recognized).
So far, I have not been told that I can't.
As for the temple - it may remained closed forever if that key is not turned.
(It may open or remain closed one way or another, but it sure seems worth a try...)
Smash the proverbial egg on the table and sail westwards to reach the East more easily.
It’s just a tiny stone idol…
ADDENDUM:
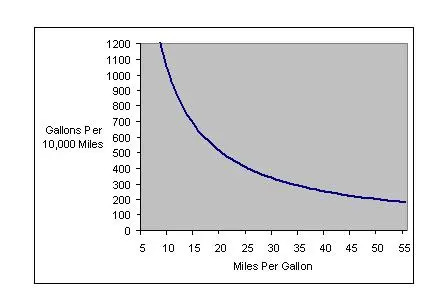
An example for an everyday use of inverted formulas would be the parallel existence of the measure of automobile performance or efficiency, in the USA as miles per gallon of fuel or mpg,
mpg = miles per gallon = distance / volume = d/v
(The higher the distance per volume ratio, the more fuel efficient that car is)
and its counterpart in Germany, Europe, where automobile mileage efficiency, or to be more precise, INefficiency is measured in liters of consumed fuel per 100 kilometers, or
liters / 100 km = volume / distance = v/d
(The higher the volume per distance ratio, the less fuel efficient that car is)
NOTE:
As this is not a law of physics, but the result of engineering, there are limits to this comparison; I put it here to show that a specific formula and its inverse can both be used to describe the same problem or phenomenon at the same time, and that the results, naturally, are inverted as well.
Both essentially mean the same thing - but one is the inverse of the other.
(But which one is "right"? Hard to say. Perhaps a hint: a combustion engine won't run without fuel, but it can idle. But then, no fuel means no distance. And one measures efficiency, the other INefficiency. So…)
An afterthought
It might becomes a bit clearer if you substitute volume with 'energy invested' and distance with (mechanical) 'work output':
Energy Invested / Work Output
E I / W O
vs.
Work Output / Energy Invested
W O / E I
Now,
the energy invested cannot be zero unless the work output is zero as well:
E I = 0 / W O > 0 // forbidden (physics) but allowed (maths)
W O > 0 / E I = 0 // forbidden (physics) and forbidden (maths) // Check
(fuel efficiency = infinite; impossible)but the work output can be zero even though the energy invested is not (all energy invested is converted to heat)
E I > 0 / W O = 0 // allowed (physics) but forbidden (maths)
W O = 0 / E I > 0 // allowed (physics) and allowed (maths) // Check
(fuel efficiency = 0; possible)
Again:
Paradoxically, any mathematically impossible ‘lone zero’ has to turn up in the denominator, if it is to match an equally impossible lone value of zero in any given physical reality;
on the other hand, any mathematically possible lone value of zero has to be in the numerator, if it is to match an even theoretically possible lone value of zero in a physical reality, such as of ‘temperature’ or ‘distance’.
So, mpg seems to have it... just like mph
So why the fuss?
Why is the inverse, gpm or gallon per mile (or liters per 100 kilometers) used elsewhere?
One answer is:
“Enhanced consumer transparency”
Just as the assumed ancient, inverse of today’s formula for speed v(i) = ‘time per distance’, as described above, makes it easier for humans to compare, to add and subtract time relative to a fixed absolute distance,
the ‘instinctive’, ‘inverse’ ratio of mpg, gpm, also makes the economic comparison, for instance, between two cars much easier than the physically correct one of mpg (which avoids the possibility of division by zero);
and since it is the relative comparison of averages, the real but single and absolute reference point of ‘zero miles’ can not and does not turn up in the denominator of the equations that are compared, thus avoiding the problem of division by zero (for the same reason, neither does ‘zero gallons’).
Here is a graph describing the difference between the two, taken from and explained in:
https://nudges.wordpress.com/why-we-misunderstand-what-miles-per-gallon-ratings-are-telling-us/
(What else? On to The Mad Matrix)