The Mad Matrix
The Forbidden Zero - A Game of choice
A ‘Blind’ Test
This still isn't exactly what I was looking for, but for the time being...:
Caveat:
I have no idea if this is valid enough to serve as a pattern or rule, or if it's just a function of pick-and-choose selection or simple coincidence.
In other words, I have no idea if there is a counterexample that would show the opposite, or otherwise inconsistent results.
The problem or task:
If given three known factors A, B, and C, is there a "blind" mechanical method for testing which of several possibilities of relation would be valid, and which would not?
And how many possibilities of relation are there at all?
The way I see it, the factors A, B, and C can be connected by multiplication in three distinct ways:
A=BC, B=AC, or C=AB
i. e. one as the result of the other two multiplied.
Expressing that relation by division is just a transformation or resolution of the above, in order:
A=BC, A=B/C, A=C/B
B=AC, B=C/A, B=A/C
C=AB, C=A/B, C=B/A
So all in all there are nine possibilities of relation; three products and six fractions.
Taking the physical formula for speed or velocity, we would have:
v=dt v=t/d v=d/t
t=dv t=d/v t=v/d
d=tv d=v/t d=t/v
(v=velocity or speed, d=distance travelled, t=time elapsed)
Checking the formula for speed
Now, focussing on the six fractions, check the mathematical formula for physical validity (all else remaining equal):
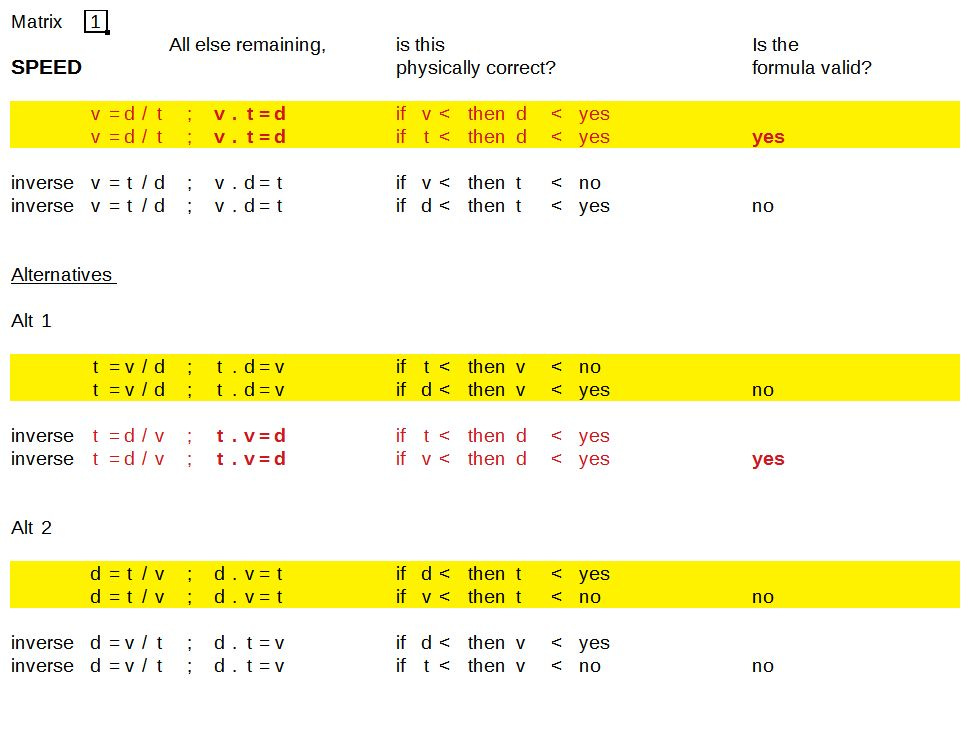
Note that the two formulas found to be valid are interchangeable; and so are three pairs of products, bringing their number back to three.
So, magically (and relying on that, hopefully, no mistakes were made), this seems to have worked out fine for the formula for speed.
Let’s check with the formula for electrical resistance (R=resistance, I=current, U=voltage):
Checking the formula for electrical resistance
Checking all possible mathematical products and fractions of three factors for physical validity (again: all else remains equal):

Again, depending on that no mistakes were made, it looks like the same result.
And so, everybody knows what’s coming: Yes, of course, the hobby horse!
Checking the formula for entropy
Everybody do their thing… I have no idea…
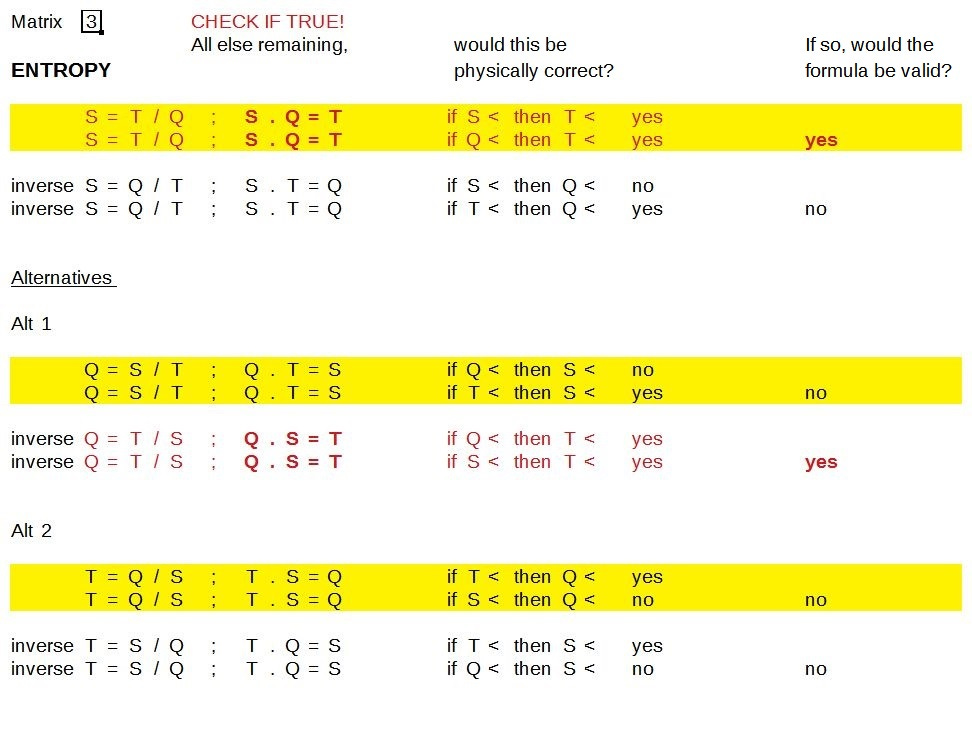
Update:
Is there a simpler rule?
Or, to try to make a simpler rule out of it, to find out if it is possible, to measure the immeasurable (such as entropy):
Can we, by pure reasoning, infer the correct relationship of any (!) three related physical quantities, by determining if each one of these variables may, or may not, take on the value of zero in real, physical terms?
Let's try
Of three quantities, A, B, and C, of which we at first know nothing, except that they are related in the form of
A=BC (equals B=A/C or C=A/B),
we assume that perhaps one, in its property as a physical quantity, may independently assume the value of zero;
then that quantity has to be placed in the numerator: in this case, A.
- this is the ‘Forbidden Zero’ -
and we assume that perhaps another, again in its property as a physical quantity, may equally independently not ever assume the value of zero;
then than that quantity must be placed in the denominator, where the value of zero may also not be assumed; in this case, either B or C.
- this is the ‘Permitted Zero’ -
If we appoint it to B, then the formula we arrive at is, again,
C=A/B or A=BC or B=A/C
in which A is possibly zero, B never is zero, and C is the dependent variable.
For speed or velocity, this would be v=d/t, with d (distance) possibly 0, and t (time) never 0; and with that, v possibly 0 as well (if d=0).
What we may NOT choose, though mathematically just as valid, is its inversion
C(i)=B/A and its derivatives B=AC(i) or A=B/C(i)
because then a physically possible zero value would turn up in the denominator (A), making it mathematically impossible, and a mathematically possible zero value in the numerator would be ruled out physically.
(Back to Mad Maths)

