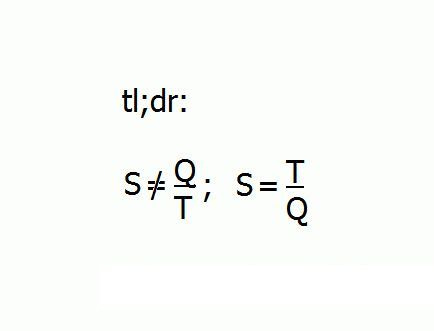Mad maths (and physics)
TL; DR:
S =/= Q/T; S = T/Q
A little math
If you want to express the relationship between two quantities A and B, you have two basically equivalent variants to choose from, which do not deliver the same results:
x = A / B
and
y = B / A.
One is the reciprocal of the other, and both variants can be equally well calculated. Both are equally valid. Mathematically.
But are they both valid physically?
Checking for the zero value:
Both expressions can then be checked, separately, to see if the value of zero might appear (solely) in the denominator of one, or the other.
That one needs to be discarded, since the expression is mathematically not defined at this point (and in physical reality not even in approximation).
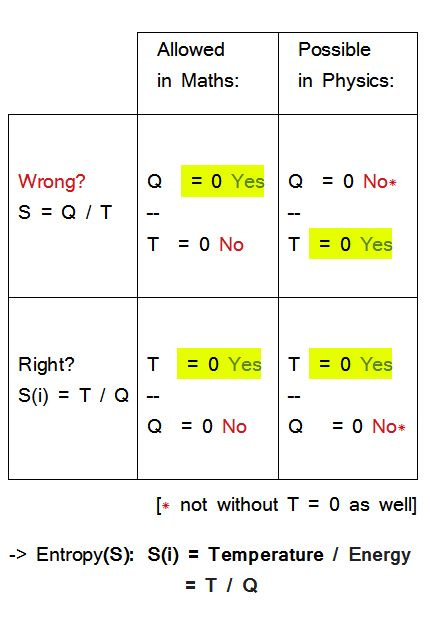
For entropy, that would be
S = Q / T
and
S(i) = T / Q
Checking denominator and numerator for zero:
Now, the formula for entropy as
S = Q / T is not defined at T = 0
(independent of Q > 0!);
On the other hand,
if Q = 0, then T = 0
(T > 0 physically causes Q > 0)
However, if one chooses the second, equally legitimate variant with the reciprocal value,
S (i) = T / Q
then everything changes:
S (i) is now defined at T = 0
(and S is zero as well!);
and if Q = 0,
T = 0 still remains mandatory.
Reality check
Cave!
We are looking at a closed system from the outside.
Now, with the conservation of energy in place, thermal and thermodynamic processes within that system will reliably cause an increase in entropy, or whatever one likes to call this new variable, via the increase in temperature.
Q, by the way, in an isolated or closed thermodynamic system, is the invariable or rather independent variable due to the law of conservation of energy; and, in the following, will be considered as such.
When calculating entropy with
S = Q / T,
the requirement is that the amount of heat or the energy content of a body or a system should be limited, in relation to the temperature. This is rather nonsense, really:
The energy content does not depend on the temperature; the latter can be zero
(undefined in the formula!).
On the other hand, as already stated, the formula theoretically allows for
Q = 0 at T > 0,
which is physically impossible.
Now using the reciprocal value,
S (i) = T / Q
the requirement is that the maximum temperature of a body or system should be limited, in relation to its amount of heat or energy content. That sounds more reasonable:
The maximum attainable temperature depends on the energy content - and that is defined.
In this formula, T = 0 is reasonable at any value of Q;
and Q is on the other hand not allowed to be 0,
especially not at T > 0
As an analogy: Speed (velocity)
As an analogy, one can employ the formula for speed (and its reciprocal value):
while the maximum distance that can be covered in a limited time is defined by the speed of light,
the maximum time that can be spent on a defined distance is not; there is no upper limit to it.
It is interesting to observe which value entropy can, and will, assume in either formula,
J / K or K / J
(for example, 0)
and what results one burning candle will deliver, as compared to two, etc. (in which the necessary reagent is often forgotten, here: oxygen).
There is also no negative entropy, as neither energy nor temperature can assume negative values (just as negative in electric terms does not mean less than zero, but less - or rather more - than on the other side, the positive one, describing a difference or potential).
Its minimum - at least theoretically - should therefore be, for entropy:
S = 0 J / K
or
S (i) = 0 K / J
but how high would the theoretical maximum be, from a physical point of view?
For every system, there should also be a maximum statistical distribution of its components, as an expression of maximum entropy.
Where is this value? As expressed in
J / K
or in its reciprocal value?
K / J
It is noteworthy that Clausius, with his presentation of the processes in a steam engine, described a measure for chaos and loss of labor potential, and not a measure of order and potential with its reciprocal value (which is not the one described here, and that is the riddle).
This makes it necessary to think in opposites: negative entropy is positive potential.
Furthermore, since a temperature difference also can (and also will be) zero over unlimited periods of time, any expression of entropy thus calculated also approaches the infinite, if this is factored in the denominator; and the amount of heat contained would be irrelevant in this regard.
It would also seem to be that with the - equally legitimate! - reciprocal value for entropy, the existence of the ordered cosmos (and life within it) changes, from an unpredictable random variable to a calculable necessity.
Clausius' thermodynamic laws have proven to be ironclad (at least in the field of thermodynamics); but in the area of entropy there may still be some fundamental contradictions and definitions to be clarified, even after 150 years.
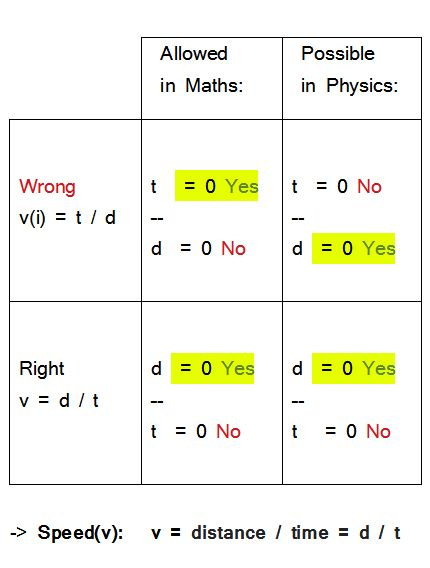
The formula for speed
The speed of light
Testing the correspondence of formula and reality and the mathematical effect of the maximum (physical) speed:
The ultimate speed or light speed corresponds to
~ 300,000 km / 1s [v = d / t]
In other words, a maximum of about 300,000 km can be covered in one second.
The time t required for any, however short distance d between two different locations in space is never zero.
An object therefore cannot be in two, and therefore all, places at the same time - and this applies, simultaneously, to all objects in the universe.
Were t = 0 possible, all objects in the universe would be everywhere at the same time; one could neither determine place, nor time, nor speed.
The value of the denominator of a fraction must never be able to assume zero, since the expression is not defined at that point - mathematically as well as physically.
If the time t in the formula for speed as
v = d / t
could be zero from a physical point of view, the state, as just described, would be physically undefinable - and mathematically as well on principle. Mathematics and reality correspond.
Mathematical requirement (denominator cannot assume zero) and physical reality (denominator cannot assume zero) match in this case.
On the other hand, the numerator, in this case distance d, must be able to assume zero for all values of time t - and indeed, an object can be immobile for any length of time.
Mathematical requirement and physical reality match again.
Cross-checking the reciprocal value
The reciprocal value of speed would be
v (i) = t / d
I. Checking the denominator:
Its value must never assume zero; here:
distance d
This however contradicts physical reality, since the distance d an object covers can physically indeed be zero for any arbitrary length of time t - in case the object does not move.
Mathematical requirement and physical reality do not correspond or match in the reciprocal formula for speed.
II. Checking the numerator:
Its value must be allowed to assume zero
(especially for a denominator above zero).
v (i) = t / d
However, time t physically cannot assume zero, as shown above.
Again, mathematical requirement and physical reality do not correspond or match, proving the reciprocal formula for speed invalid for both cases (and recommending this test for future evaluations).
It could also be stated that the more independent value should be in the denominator, but which cannot easily be determined that way.
The template
[Both solutions are mathematical valid, but what is allowed in the realm of mathematics must also be possible in the material world of physics, and what is forbidden in mathematics must also be impossible in the real world as well; and vice versa.]
Testing for one factor being able to assume the value of zero independent of the other:
Picking it apart
Before, the distance was considered to be the ‘independent’ variable; it could not be changed: it was static, as the environment is. The time used to cover that distance was dependent on the speed of travel v(i) - or vice versa: the speed differed, depending on the elapsed time.
Note that v is inversely proportional to the time taken: halving the time doubles the speed, doubling the speed halves the time; while v(i) rises with time.
In that former, rather more natural way of thinking, actual speed is something arrived at only with some additional, somewhat convoluted internal calculations such as “As the army, message… (or whatever) arrived here in half the time, they must have moved at twice the speed”.
These “convoluted calculations“ can be seen as a result of a „wrong“ formula in which speed v(i) is not the actual result, but rather something one might call duration, which then has to be translated into speed.
That changed when Galileo Galilei (or whoever it was) set the focus on the dynamic moving object, making time the independent variable, and the distance covered in that time dependent on the speed v.
Note that v is now directly proportional to the distance covered: doubling the distance doubles the speed. Speed is now the direct result of the „right“ formula, which focuses on the dynamically moving object and regards the elapsed time as static and independent, and the distance covered as the dependent variable, i. e. depending on the speed or velocity v of the moving object.
Note also that the variable regarded as „independent“ turns up as the denominator in both cases. (There may even be a rule here, i. e. „The variable regarded as 'independent' must always turn up in the denominator“ but I have not been able to work that one out yet.)
Apparently, however, the formula for speed in its valid, current form as v=d/t - and measured in km/h or mph, for example - has only been in existence for around 500 years; its formulation is attributed to Galileo Galilei (or a contemporary).
From then on, the modern physics and modern engineering began to take hold.
That begs the question:
What was before?
Presumably, in fact, it might very well have been its inversion, v(i)=t/d, namely an indication of the time necessary to cover a certain distance, without being able to handle this in a mathematically stringent way.
Even today, we instinctively indicate a time when we are asked "how fast" something (or someone) travels from one place to another:
The package will be there in three days, you would need ten minutes to reach a certain goal, etc.; in other words, an indication of the time per route:
v (i) = t / d
This, again presumably, may have been because, since the invention of language, it was not the (usually invariable) distance that was decisive for human life, but the variable time that was needed to overcome it; for example as "a day's march".
An army needed so and so many days from here to there, a fleet across the sea so many weeks; depending on the means of transport, a package or a message takes so and so long to get to the recipient.
(Time can also used to describe how quickly a job is done, thus describing performance; but that would be another topic.)
It was only when speed was transferred to the uniform movement of a mechanical object, for example an arrow, did the reciprocal value of this information - the current expression for "speed" - suddenly made sense:
v = d / t
Now, suddenly, immobility could be mathematically described, since
d = 0
had been shifted into the numerator; and the physically impossible
t = 0
was now mathematically equally undefined as denominator (that an object cannot physically be in two places at the same time has generally always been known).
Once more to the case of entropy
Once again, let's assume that the variable regarded as „independent“ turns up as the denominator in both variants of the formula, the original and the alternative above.
If so, the current or rather original formula for Entropy S=Q/T regards the Temperature T as “independent”, and the Energy Q contained in the system or object as “dependent”, which seems a bit weird from the start.
But what really IS “entropy”?
In first describing it, the German physicist and mathematician Rudolf Clausius called it the "transformative content"of a body or system in thermodynamics.
It has also been described as the “inability to do work” or “thermal energy per unit temperature that is unavailable for doing useful work”, or similar negative and, to be honest, strangely humanizing, if not accusatory expressions, while at the same time elevating it to almost a religious deity within science, and breaking their minds over it.
Why should one bother with or even worship an “inability” or “unavailability” instead of looking to describe the opposite? The observable outcome of this obsession, in any case, was extraordinarily nihilistic and defeatist.
And again, we are confronted with a “convoluted” way of thinking which is possible, but extremely complicated to perform, and leads to vague, manipulated or contradictory results. This, too, can be seen as the result of a valid, but “wrong” formula.
This is similar to measuring the inefficiency of a car or other machine.
However, if one reduces it to the basics, entropy S is nothing but the relation of the “mean kinetic energy” of the molecules or atoms, which translates into absolute temperature T, to the overall potential energy Q contained in that body or system of said temperature; in other words, the part of the energy already used (or released!) in relation to the part still available:
In a car, you burn a tank full of fuel with air to get from A to B, and their common temperature will rise in negative proportion of the fuel still available, in everyday life giving you an idea at a glance on the gage on how much you have already used and how much you have left to reach your destination.
It is not the “unavailability” or “inability” you are gaging, but the part still available to you and, of course, subtracted from that, the part no longer available and useful to you, but which got you to where you are now.
Returning to the formula, the current or original one
S=Q/T thus translates to
Entropy = Potential Energy (available) / Kinetic Energy (released)
while the alternative one
S=T/Q translates to
Entropy = Kinetic Energy (released) / Potential Energy (available)
and apart from anything else, the second one seems more reasonable: in it, for instance, a Temperature of T=0 would indicate you have not used any potential at all yet, and so your entropy is also the lowest possible (zero); and while the interpretation of the original formula may seem more natural, using the formalistic template of the formula for speed above, it is hard to explain or justify.
Work it out for yourself:
Again, testing for one factor being able to assume the value of zero independent of the other:
[Note again: Temperature requires Energy; an object with a temperature above 0K cannot have an energy content of 0 either, while an object with a (potential) energy content above 0 can still have a temperature of 0K.]
Epilogue
If, for some, the Yin-Yang outlook of the giving versus the receiving, the order-creating and the order-destroying, the relationship between the gravitational and the thermodynamic systems may seem too esoteric, then so be it. Over the millennia, people have had to express, and pass on, their perception of their surroundings in a limited language, one way or another.
The very concrete background (abstract as it is) to this is presented in the molecular movement:
In the thermodynamic realm, the molecular movement is undirected, it takes place in a completely disordered manner; this is a feature which is so stable that deviations from it lead to statistical statements. It is on this area of fundamental disorder that science has based its philosophy over the past 150 years.
Indeed, in the realm of disorder, order is a deviation; and if you depend on it, a frighteningly rare exception.
In the gravitational realm, on the other hand, since a force is in effect, any movement is directed right from the beginning; and the longer this force acts over time, the stronger it becomes, and the even more directed the movement becomes as well, until finally everything moves towards a point - and this principle of self-reinforcement also stands in direct contrast to the self-reducing degradation seen in thermodynamic processes.
This direction of movement, too, is so stable that man-made space probes can be sent to celestial bodies far away, over a stretch of many years, and hit them on the point and to the minute. Still, oddly enough, science has never attempted to make a philosophy out of it; and if so, then this attempt was discredited by thermodynamists, who pride in having defeated entropy in the very existence of themselves, on ridiculous pretexts.
But it is, what it is:
The victory over thermodynamics cannot be thermodynamic - their very own laws forbid it.
The apologists know this very well; hence the denial of their own thermodynamic condition, as it finds its expression in the thermodynamic dissolution of one's own body before and after death; their denial of the order necessary for their existence is in defense against their own existential fear: You can only deny something you know to exist.
The victory over thermodynamics, and thus over chance (and thus over decay), can only be of non-thermodynamic origin; and perhaps, as suggested here, gravitational.
Under the influence of a force such as gravity (whose peculiarity is that it depends exclusively on the existence of matter), undirected movement becomes directed, and chaos becomes order.
This result then, spawns the esoteric view:
The Yin and Yang, the give and take.
The universe being aligned.
- - -
(on to thoughts & elaborations / the mad matrix)